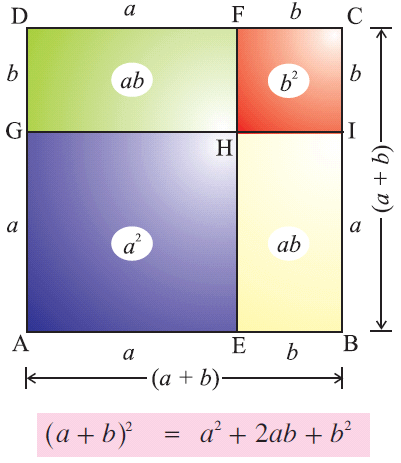
在文节中,您将学习(a + b)2的公式或展开。
那是,
(a + b)2 =(a + b)(a + b)
(a + b)2 = a 2 + ab + ab + b 2
(a + b)2 = a 2 + 2ab + b 2
用几何证明正整数b的展开
在本节中,我们将看到如何以 几何方式证明 (a + b)2的展开。
我们可以 使用正方形的面积证明(a + b)2的展开,如下所示。
解决的问题
问题1:
展开:
(x + y)2
解决方案:
(x + y)2 的形式为(a + b)2
比较 (a + b)2 和 (x + y)2 ,我们得到
a = x
b = y
写出(a + b)2的公式/展开 。
(a + b)2 = a 2 + 2ab + b 2
将x替换为a,将y替换为b。
(x + y)2 = x 2 + 2(x)(y)+ y 2
(x + y)2 = x 2 + 2xy + y 2
因此, (x + y)2的展开 是
x 2 + 2xy + y 2
问题2:
展开:
(x + 2)2
解决方案:
(x + 2)2 的形式为(a + b)2
比较 (a + b)2 和(x + 2)2,我们得到
a = x
b = 2
写出(a + b)2的公式/展开 。
(a + b)2 = a 2 + 2ab + b 2
将x替换为a,将2替换为b。
(x + 2)2 = x 2 + 2(x)(2)+ 3 2
(x + 2)2 = x 2 + 4x + 9
因此, (x + 2)2的展开 是
x 2 + 4x + 9
问题3:
展开:
(5x + 3)2
解决方案:
(5x + 3)2 的形式为(a + b)2
比较 (a + b)2 和(5x + 3)2,我们得到
a = 5倍
b = 3
写出 (a + b)2的展开式。
(a + b)2 = a 2 + 2ab + b 2
用5x替换a,用3替换b。
(5x + 3)2 =(5x)2 + 2(5x)(3)+ 3 2
(5x + 3)2 = 25x 2 + 30x + 9
因此, (5x + 3)2的展开 是
25x 2 + 30x + 9
问题4:
如果a + b = 7且a 2 + b 2 = 29,则求ab的值。
解决方案:
要获得ab的值,我们可以使用(a + b)2的公式或扩展 。
写出(a + b)2的公式/展开 。
(a + b)2 = a 2 + 2ab + b 2
要么
(a + b)2 = a 2 + b 2 + 2ab
将(a + b)替换为7,将(a 2 + b 2)替换为29 。
7 2 = 29 + 2ab
49 = 29 + 2ab
每边减去29。
20 = 2ab
将每一边除以2。
10 =绝对
因此,ab的值为10。
问题5:
查找以下值:
(√2+ 1 /√2)2
解决方案:
(√2+ 1 /√2)2的形式为(a + b)2
比较 (a + b)2 和 (√2+(1 /√2)2 ,我们得到
a = √2
b = 1 / √2
写出 (a + b)2的展开式。
(a + b)2 = a 2 + 2ab + b 2
用 √2 代替a和1 / √2 代替b。
(√2 + 1 / √2)2 =(√2 )2 + 2(√2 )(1 / √2 )+(1 / √2)2
(√2 + 1 / √2)2 = 2 + 2 + 1/2
(√2+ 1 /√2)2 = 9/2
因此, (√2+ 1 /√2)2的值是
9/2
问题6:
查找以下值:
(105)2
解决方案:
不用将105乘以105得到(105)2的值,我们可以使用(a + b)2的代数公式,轻松地找到(105)2 的值。
写入 (105)2 中的(A + B)的形式2。
(105)2 =(100 + 5)2
写出 (a + b)2的展开式。
(a + b)2 = a 2 + 2ab + b 2
将100替换 为a,将5替换 为b。
(100 + 5 )2 =(100 )2 + 2(100)(5 )+(5 )2
(100 + 5 )2 = 10000 + 1000 + 25
(10 5 )2 = 11025
因此,(10 5 )2的值 是
11025
代数恒等式
代数恒等式是相等的, 不管其中出现的任何变量的值如何,都保持不变。
更新:20210423 104205查看下面更多的实例题